Category Archives: Differential Equations

Differential Equations, Math

Oryx population example

Leave a comment

I will show how to solve a classical problem of modeling a oryx population using differential equations. The problem says:

An African government is trying to come up with a good policy regarding the hunting of oryx. They are using the following model: the oryx population has a natural rowth rate of k years^-1, and there is assumed a constant harvesting rate of a oryxes/year. Tasks:

  1. Write down a model for the oryx population.
  2. Suppose a=0. What is the doubling time?
  3. Find the general solution of this equation.
  4. Check that the proposed solution satisfies the ODE.
  5. There is a constant solution. Find it.
  6. Graph the constant solution (equilibrium) and some others, Why, in this case, do we say the constant solution is “unstable”?
  1. growth rate: k\, {year}^{-1}
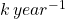
    harvesting rate: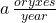 a\, \frac{oryxes}{year}
    Let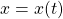 x=x(t) be the population of oryxes at time t.

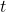    We can think as the change of oryxe population in a time interval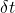 \delta{t} to be the result of the growth rate multiplied by the current population 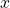x and by the time interval. And the decrease in population represented with a minus sign with the harvesting rate multiplied by the time interval. So we have:

    \[\Delta{x}=k*x*\Delta{t}-a*\Delta{t} \\\frac{\Delta{x}}{\Delta{t}}=k*x\]