All posts by saenzac

Differential Equations, Math

Oryx population example

Leave a comment

I will show how to solve a classical problem of modeling a oryx population using differential equations. The problem says:

An African government is trying to come up with a good policy regarding the hunting of oryx. They are using the following model: the oryx population has a natural rowth rate of k years^-1, and there is assumed a constant harvesting rate of a oryxes/year. Tasks:

  1. Write down a model for the oryx population.
  2. Suppose a=0. What is the doubling time?
  3. Find the general solution of this equation.
  4. Check that the proposed solution satisfies the ODE.
  5. There is a constant solution. Find it.
  6. Graph the constant solution (equilibrium) and some others, Why, in this case, do we say the constant solution is “unstable”?
  1. growth rate: k\, {year}^{-1}
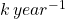
    harvesting rate: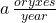 a\, \frac{oryxes}{year}
    Let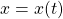 x=x(t) be the population of oryxes at time t.

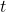    We can think as the change of oryxe population in a time interval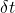 \delta{t} to be the result of the growth rate multiplied by the current population 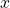x and by the time interval. And the decrease in population represented with a minus sign with the harvesting rate multiplied by the time interval. So we have:

    \[\Delta{x}=k*x*\Delta{t}-a*\Delta{t} \\\frac{\Delta{x}}{\Delta{t}}=k*x\]

Linux

CREATE DB, dump and restore postgresql database

Leave a comment

I will show how to create a new database (DB) with some user credentials and then a migration will be done. The migration consists of copying an entire database (DB) from one to another computer.

Creating a new DB:

The “openproject” database and a user of the same name are created. The user privileges are given to the new database and finally a password is set for the user.

$ sudo -u postgres psql
$ postgres= create database openproject;
$ postgres= create user openproject;
$ postgres= grant all privileges on database "openproject" to openproject;
$ postgres= alter user openproject with password 'new_password' ;

Then wen can make changes to the newly created database.

Create the backup with pg_dump command:

We make a backup of our “openproject” database with the following command. It include blobs, if any in our database.

$ pg_dump -h localhost -p 5432 -U postgres -F c -b -v -f  <backup path> <database name>

-F c is custom format (compressed, and able to do in parallel with -j N)
-b is including blobs,
-v is verbose
-f is the backup file name

Restore the backup with

We can restore a previously backup database with the following command.

$ pg_restore -h localhost -p 5432 -U postgres -d  -v <backup file name>

Just make sure the DB name is the same in both commands and that the destination DB is created before using pg_restore. And create the DB with the same user credentials as the original DB.

Control

system identification using excel

Leave a comment

In this article we will show how to do a third order system identification using excel. The identification takes place in the Laplace domain (\mathcal{L{}}) where the optimal system parameters are found by using the gradient descend method.

Consider the following second order system, a DC motor for example:

    \[ Y(s) = \frac{1}{a_3 s^3 + a_2 s^2 + a_1 s} V(s)\]

Where a_{3}^*, a_{2}^*, a_{1}^* are the optimal parameters to be found by minimizing the cost function:

Transforming the system to the Z-domain by using Euler’s forward approximation:


    \[ \frac{Y(z)}{V(z)} = \frac{a z^{-3}}{-z^{-3} b - c z^{-2} - d z^{-1} + 1 } \]

Which leads to the following difference equations:

The cost function to be minimized is :

The validation shows a satisfactory match between the estimated and the real model:

$ls
postfix.txt
&gt; Johnny